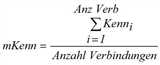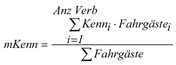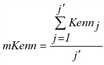Je nach gewähltem Suchverfahren gibt es unterschiedliche Möglichkeiten, die Kenngrößen (Kenn) der Verbindungen zu mittleren Kenngrößen (mKenn) je Beziehung zusammenzufassen (Tabelle 171).
|
Funktionen der Aggregation |
Taktfein |
FP-fein |
|
ungewichtetes Quantil Für 0 ≤ z ≤ 1 ist ein z-Quantil einer endlichen, geordneten Folge von Werten (x1, ..., xn) definiert als die kleinste Zahl y, für die gilt, dass # {i : xi ≤ y } / n ≥ z ist. |
X |
X |
|
gewichtetes Quantil Die Verbindungen werden bei der Berechnung des Quantils mit der Belastung gewichtet. |
X |
X |
|
ungewichtetes Mittel
|
X |
X |
|
gewichtetes Mittel
|
X |
X |
|
ungewichtetes Mittel eingeschränkt auf Wege mit hinreichend niedrigem Widerstand
|
X |
X |
|
gewichtetes Mittel eingeschränkt auf Wege mit hinreichend niedrigem Widerstand
|
X |
X |
|
mKenn = Kennwert für Route mit minimalem Widerstand |
X |
|
|
mKenn = Kennwert für Route/Verbindung mit minimaler empfundener Reisezeit |
|
X |
Tabelle 171: Zusammenfassung von Kenngrößen zu mittleren Kenngrößen je Beziehung
|
Hinweis: Bei der Berechnung eines gewichteten Mittels werden standardmäßig die Gewichte in der Kenngrößenberechnung gebildet. Dafür wird die Nachfrage in den Ganglinienintervallen zur Gesamtnachfrage im Umlegungszeitraum ins Verhältnis gesetzt. Wenn die Gewichte bei einer prozentualen Ganglinie im Umlegungszeitraum null ergeben bzw. die Summe der Nachfrage aus einer Matrixganglinie für eine Quelle-Ziel-Beziehung im Umlegungszeitraum null ist, wird eine feste Nachfrage angenommen und das jeweilige Zeitintervall mit seiner Länge im Verhältnis zum Umlegungszeitraum gewichtet. |
Die Kenngröße Bedienungshäufigkeit BDH bezieht sich nicht auf einen einzelnen Weg oder eine Verbindung, sondern auf eine Quelle-Ziel-Beziehung.
Beispiel
Für eine Quelle-Ziel-Beziehung werden drei Verbindungen ermittelt:
|
Verbindung |
1 |
2 |
3 |
|
Belastung |
50 % |
20 % |
30 % |
|
Umsteigehäufigkeit |
1 |
3 |
2 |
Die Umsteigehäufigkeit der Quelle-Ziel-Beziehung berechnet sich mit den verschiedenen Aggregationsfunktionen folgendermaßen:
|
Mittelwert |
50 %-Quantil |
||
|
ungewichtet |
gewichtet |
ungewichtet |
gewichtet |
|
(1 + 3 + 2) / 3 = 2 |
1 • 0,5 + 3 • 0,2 +2 • 0,3 = 1,7 |
Werte: (1, 2, 3) 50 %-Quantil = 2 |
Werte: (1,1,1,1,1,2,2,2,3,3) 50 %-Quantil = 1 |